Home  ›  Difference in Means Between Two Chi Square Distribution Continuous Outcome

Difference in Means Between Two Chi Square Distribution Continuous Outcome

Written By Sunday, October 16, 2022 Add Comment Edit

A random variable has a Chi-square distribution if it can be written as a sum of squares of independent standard normal variables.

Sums of this kind are encountered very often in statistics, especially in the estimation of variance and in hypothesis testing.

In this lecture, we derive the formulae for the mean, the variance and other characteristics of the chi-square distribution.

Table of Contents

Table of contents

  1. Degrees of freedom

  2. Definition

  3. Symbol

  4. Expected value

  5. Variance

  6. Moment generating function

  7. Characteristic function

  8. Distribution function

  9. More details

    1. The sum of independent chi-square random variables is a Chi-square random variable

    2. The square of a standard normal random variable is a Chi-square random variable

    3. The sum of squares of independent standard normal random variables is a Chi-square random variable

  10. Density plots

    1. Plot 1 - Increasing the degrees of freedom

    2. Plot 2 - Increasing the degrees of freedom

  11. Solved exercises

    1. Exercise 1

    2. Exercise 2

    3. Exercise 3

We will prove below that a random variable X has a Chi-square distribution if it can be written as [eq1] where $Y_{1}$ , ..., $Y_{n}$ are mutually independent standard normal random variables.

The number n of variables is the only parameter of the distribution, called the degrees of freedom parameter. It determines both the mean (equal to n ) and the variance (equal to $2n$ ).

Chi-square random variables are characterized as follows.

To better understand the Chi-square distribution, you can have a look at its density plots.

The following notation is often employed to indicate that a random variable X has a Chi-square distribution with n degrees of freedom: [eq6] where the symbol $symbol{126}$ means "is distributed as".

The expected value of a Chi-square random variable X is [eq7]

Proof

It can be derived as follows: [eq8]

The proof above uses the probability density function of the distribution. An alternative, simpler proof exploits the representation (demonstrated below) of X as a sum of squared normal variables.

Proof

The variance of a Chi-square random variable X is [eq12]

Proof

Again, there is also a simpler proof based on the representation (demonstrated below) of X as a sum of squared normal variables.

Proof

The moment generating function of a Chi-square random variable X is defined for any $frac{1}{2}$ : [eq18]

Proof

The characteristic function of a Chi-square random variable X is [eq20]

Proof

Using the definition of characteristic function, we obtain: [eq21]

The distribution function of a Chi-square random variable is [eq22] where the function [eq23] is called lower incomplete Gamma function and is usually computed by means of specialized computer algorithms.

Proof

This is proved as follows: [eq24]

Usually, it is possible to resort to computer algorithms that directly compute the values of [eq25] . For example, the MATLAB command

chi2cdf(x,n)

returns the value at the point x of the distribution function of a Chi-square random variable with n degrees of freedom.

In the past, when computers were not widely available, people used to look up the values of [eq26] in Chi-square distribution tables, where [eq27] is tabulated for several values of x and n (see the lecture entitled Chi-square distribution values).

In the following subsections you can find more details about the Chi-square distribution.

The sum of independent chi-square random variables is a Chi-square random variable

Let X_1 be a Chi-square random variable with $n_{1}$ degrees of freedom and X_2 another Chi-square random variable with $n_{2}$ degrees of freedom. If X_1 and X_2 are independent, then their sum has a Chi-square distribution with $n_{1}+n_{2}$ degrees of freedom: [eq28] This can be generalized to sums of more than two Chi-square random variables, provided they are mutually independent: [eq29]

Proof

The square of a standard normal random variable is a Chi-square random variable

Let Z be a standard normal random variable and let X be its square: [eq34] Then X is a Chi-square random variable with 1 degree of freedom.

Proof

For $xgeq 0$ , the distribution function of X is [eq35] where [eq36] is the probability density function of a standard normal random variable: [eq37] For $x<0$ , [eq38] because X , being a square, cannot be negative. Using Leibniz integral rule and the fact that the density function is the derivative of the distribution function, the probability density function of X , denoted by [eq39] , is obtained as follows (for $xgeq 0$ ): [eq40] For $x<0$ , trivially, [eq41] . As a consequence, [eq42] Therefore, [eq43] is the probability density function of a Chi-square random variable with 1 degree of freedom.

The sum of squares of independent standard normal random variables is a Chi-square random variable

Combining the two facts above, one trivially obtains that the sum of squares of n independent standard normal random variables is a Chi-square random variable with n degrees of freedom.

This section shows the plots of the densities of some Chi-square random variables. These plots help us to understand how the shape of the Chi-square distribution changes by changing the degrees of freedom parameter.

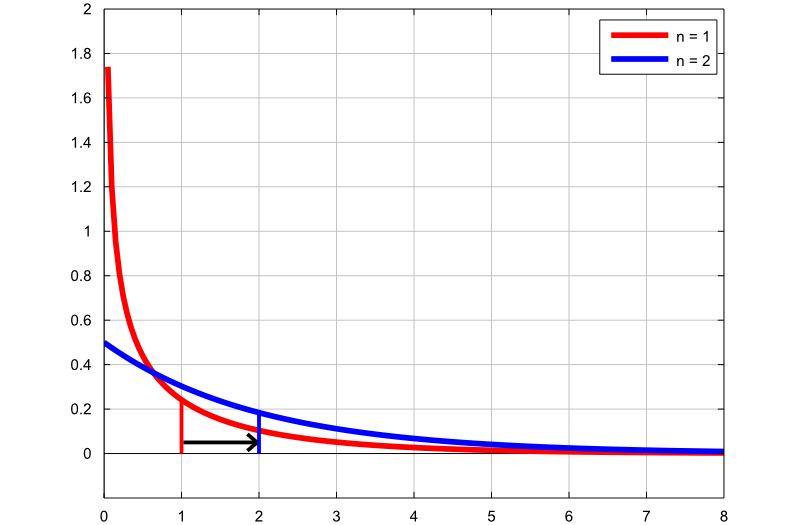
Plot 1 - Increasing the degrees of freedom

The following plot contains the graphs of two density functions:

  • the first graph (red line) is the probability density function of a Chi-square random variable with $n=1$ degrees of freedom;

  • the second graph (blue line) is the probability density function of a Chi-square random variable with $n=2$ degrees of freedom.

The thin vertical lines indicate the means of the two distributions. By increasing the number of degrees of freedom, we increase the mean of the distribution, as well as the probability density of larger values.

Chi-square density plot 1

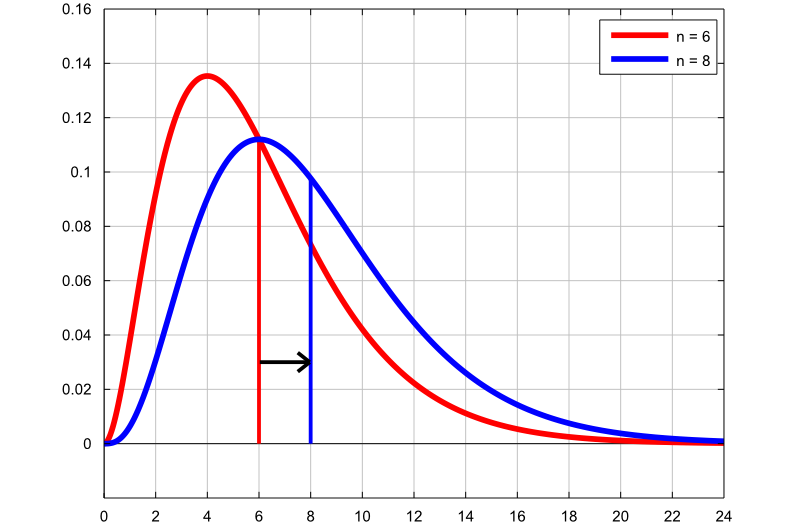
Plot 2 - Increasing the degrees of freedom

The following plot also contains the graphs of two density functions:

  • the first graph (red line) is the probability density function of a Chi-square random variable with $n=6$ degrees of freedom;

  • the second graph (blue line) is the probability density function of a Chi-square random variable with $n=8$ degrees of freedom.

As in the previous plot, the mean of the distribution increases as the degrees of freedom are increased.

Chi-square density plot 2

Below you can find some exercises with explained solutions.

Exercise 1

Let X be a chi-square random variable with $3$ degrees of freedom.

Compute the following probability: [eq44]

Solution

First of all, we need to express the above probability in terms of the distribution function of X : [eq45] where the values [eq46] can be computed with a computer algorithm or found in a Chi-square distribution table (see the lecture entitled Chi-square distribution values).

Exercise 2

Let X_1 and X_2 be two independent normal random variables having mean $mu =0$ and variance $sigma ^{2}=16$ .

Compute the following probability: [eq47]

Solution

First of all, the two variables X_1 and X_2 can be written as [eq48] where $Z_{1}$ and $Z_{2}$ are two standard normal random variables. Thus, we can write [eq49] but the sum [eq50] has a Chi-square distribution with $2$ degrees of freedom. Therefore, [eq51] where [eq52] is the distribution function of a Chi-square random variable Y with $2$ degrees of freedom, evaluated at the point $frac{1}{2}$ . With any computer package for statistics, we can find [eq53]

Exercise 3

Suppose that the random variable X has a Chi-square distribution with $5$ degrees of freedom.

Define the random variable Y as follows: [eq54]

Compute the expected value of Y .

Solution

The expected value of Y can be easily calculated using the moment generating function of X : [eq55] Now, by exploiting the linearity of the expected value, we obtain [eq56]

Please cite as:

Taboga, Marco (2021). "Chi-square distribution", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/probability-distributions/chi-square-distribution.

davyinare1949.blogspot.com

Source: https://www.statlect.com/probability-distributions/chi-square-distribution

0 Response to "Difference in Means Between Two Chi Square Distribution Continuous Outcome"

Post a Comment

Subscribe to: Post Comments (Atom)

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel